Wybrane metody pozwalające na zmianę wielkości liter i obliczenie długości stringów w Pythonie. Po # efekt działania polecenia w Pythonie.
napis = 'Witaj'
print(napis.upper()) # WITAJ
print(napis.lower()) # witaj
print(len(napis)) # 5
Wybrane metody pozwalające na zmianę wielkości liter i obliczenie długości stringów w Pythonie. Po # efekt działania polecenia w Pythonie.
napis = 'Witaj'
print(napis.upper()) # WITAJ
print(napis.lower()) # witaj
print(len(napis)) # 5
Modyfikacja elementów listy
Możemy dodać nowy element do listy podając indeks istniejącego elementu i przypisując mu nową wartość. Elment listy o indeksie 2 zostanie zastąpiony nowym elementem, a więc lista będzie miała tyle samo elementów, co wcześniej
lista[2] = 4
Dodawanie elementów do listy
Jeżeli chcemy rozszerzyć listę o nowy element pozostawiając wszystkie poprzednie elementy musimy zastosować metodę append
lista.append(6)
Spowoduje to dodanie cyfry 6 na końcu listy.
Innym sposobem rozszerzenia listy jest metoda extend. Przy jej pomocy można jednocześnie dodać jeden lub więcej elementów.
lista.extend([2])
lub
lista.extend([2],[7])
Listy w Pythonie można sortować za pomocą metody sort(). Metoda ta sortuje elementy listy w miejscu, czyli modyfikuje oryginalną listę.
np. lista = [3, 1, 2]
lista.sort()
print(lista) da efekt [1, 2, 3]
Bardzo łatwo można znaleźć najmniejszą i największą liczbę na liście.
np. lista = [3, 1, 2]
print(min(lista)) # tutaj da wynik 1
print(max(lista)) # a tutaj 3
W języku Python do przechowywania wielu danych w jednej zmiennej służą listy. Elementami listy mogą być liczby, napisy, inne listy. Możemy stworzyć listę podając obiekty, z których się składa.
Tak możemy utworzyć listę, w której zapiszemy liczby:
liczby = [33, 56, 77]
print(liczby)
A tak tworzymy listę z napisami:
napisy = ['Ala', 'Ola', 'Ewa']
print(napisy)
Przy pomocy poznanego wcześniej indeksowania możemy odwołać się do konkretnego obiektu w liście.
liczby = [33, 56, 77]
print(liczby[1])
wynik:
56
lub
napisy = ['Ala', 'Ola', 'Ewa']
print(napisy[-1])
wynik:
Ewa
Aby odczytać ciąg elementów na liście, należy podać numer indeksu, od którego mają zostać odczytane elementy z listy oraz dwukropek. Wówczas odczytane zostaną wszystkie elementy, zaczynając od wskazanego indeksu aż do końca listy np.
napisy = ['Ala', 'Ola', 'Ewa', 'Marta', 'Anna']
print(napisy[1:])
da wynik:
['Ola', 'Ewa', 'Marta', 'Anna']
Jeśli potrzebujemy uzyskać dostęp do części listy, możemy skorzystać z dwukropka. Po nazwie listy należy podać w nawiasach kwadratowych pozycję pierwszego elementu, dwukropek oraz liczbę o jeden większą od ostatniego elementu w wybranym fragmencie.
napisy = ['Ala', 'Ola', 'Ewa', 'Marta', 'Anna']
print(napisy[1:4])
da wynik:
['Ola', 'Ewa', 'Marta']
Jeśli wyodrębniany fragment zaczyna się od początku listy lub kończy się ostatnim elementem, liczbę pomijamy.
napisy = ['Ala', 'Ola', 'Ewa', 'Marta', 'Anna']
print(napisy[:4])
da wynik:
['Ala', 'Ola', 'Ewa', 'Marta']
W Pythonie są trzy struktury danych, które są sekwencjami, to znaczy przechowują dane w postaci uporządkowanych szeregów wartości. W sekwencji każda wartość jest na określonej pozycji. Dzięki temu możesz odwołać się do pojedynczej wartości w sekwencji używając numeru jej pozycji, czyli indeksu.
Indeks elementu sekwencji podaje się w nawiasach kwadratowych po samej sekwencji lub po nazwie zmiennej, która na tę sekwencję wskazuje. Najprostszymi sekwencjami są łańcuchy znaków - składają się bowiem z uporządkowanego szeregu znaków, z których każdy ma swoją określoną pozycję. Elementy w sekwencjach numerowane są od 0 (zera) np.
tekst = "informatyka"
print(tekst[2])
da wynik:
f
Dlaczego? Bo element łańcucha "informatyka" o indeksie [2] jest tak naprawdę trzecim elementem w tym łańcuchu znaków. Numeracja zaczyna się od zera!

Do elementów sekwencji możemy odwołać się także od prawej strony uzywając indeksów ujemnych.
tekst = "informatyka"
print(tekst[-2])
da wynik:
k
Możemy łączyć łańcuchy.
imie = "Bill"nazwisko = "Gates"razem = imie + " " + nazwiskoprint(razem)Bill Gatesimie = "Bill"nazwisko = "Gates"razem = imie[-1] + nazwisko[1] + nazwisko[-1]print(razem)lasPętlę for znacie ze Scratcha. Tam wyglądało to tak:
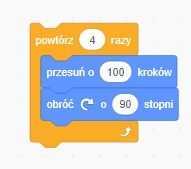
Iteracja (łac. iteratio – powtarzanie) – czynność powtarzania tej samej operacji w pętli z góry określoną liczbę razy lub aż do spełnienia określonego warunku. Mianem iteracji określa się także operacje wykonywane wewnątrz takiej pętli.
np.
for i in [0, 5, 2, 8, 4]: print(i)
W wyniku działania tego programu zmienna i przybierze najpierw wartość 0, w następnym kroku 5, później 2 itd.
Każda z tych wartości zostanie wyprowadzona instrukcją wyjścia (print) na ekran. ZWRÓĆ UWAGĘ na znak dwukropka na końcu oraz cztery spacje wcięcia!
for i in range(5): print(i)
uwaga! range oznacza zakres
W tym przypadku zamiast wypisywać listę wartości korzystamy z funkcji range(), która wygeneruje kolejne liczby całkowite od 0 aż do napotkania na koniec czyli 5.
W wyniku działania tego programu wyświetlą się na ekranie kolejno 0, 1, 2, 3 i 4. Funkcja range() z wpisanym wewnątrz nawiasu jednym argumentem traktuje go jako koniec pętli i nie wyświetla.
Jeżeli chcemy wyświetlić jakiś konkretny przedział liczb to możemy w range() podać początek i koniec tego przedziału. Koniec znów się nie wyświetli.
for i in range(5, 10): print(i)
Ten program wyświetli kolejno: 5, 6, 7, 8, i 9.
Ale range() może mieć 3 argumenty: początek, koniec i krok.
for i in range(5, 16, 5): print(i)
W tym przypadku program wyświetli kolejno: 5, 10 i 15, bo koniec to 16, a krok to 5.
Jeżeli chciałbym wyświetlić na ekranie liczby całkowite ale w odwrotnej kolejności to mogę zastosować krok ujemny, oczywiście należy wpisać również początek i koniec.
for i in range(15, 4, -5): print(i)
W tym przypadku zmienna i będzie przybierała w kolejnych krokach następujące wartości: 15, 10, 5. Koniec to 4, a krok jest ze znakiem minus.
p = int(input("Podaj wartość całkowitą zmiennej p: "))k = int(input("Podaj wartość całkowitą zmiennej k: "))step = int(input("Podaj wartość całkowitą zmiennej krok: "))
for i in range(p, k, step): print(i)
A w tym programie pytam użytkownika o początek, koniec i krok dla funkcji range().
for i in range(5): a = int(input("Podaj wartość a: "))
Taki program zapyta użytkownika 5 razy o wartość zmiennej a.
for i in range(5): print("Ala ma kota")
A ten program napisze 5 razy Ala ma kota.
napis = "szkola"
for litera in napis:
print(litera)
W tym programie zdefiniowano zmienną typu string o nazwie napis. A następnie w pętli odczytujemy litera po literze zmienną napis i drukujemy litery na ekranie.
Poniższa instrukcja importuje bibliotekę o nazwie random.
import random
Na lekcjach korzystamy często z funkcji randint wchodzącej w skład w/w biblioteki random.
Aby wywołać randint musimy użyć polecenia np.
los = random.randint(1, 5) # polecenie wylosuje liczbę z zakresu od 1 do 5 i zapamięta ją w zmiennej o nazwie los
Jeżeli chcemy zaimportować konkretne polecenie z biblioteki random np. tylko randint piszemy:
from random import randint
wtedy już tylko
los = randint(1, 5)
i jak widać bez random.
Poniższy zapis zaimportuje wszystkie funkcje z biblioteki random i w tym przypadku również nie będzie konieczne poprzedzanie ich random.
from random import *
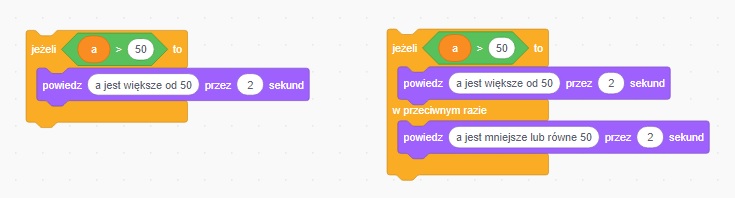
Dzięki instrukcji warunkowej if możesz wykonać blok instrukcji w zależności od tego, czy wyrażenie po if ma wartość True (Prawda).
Składnia:
if warunek_logiczny: instrukcja_1 instrukcja_2 instrukcja_3 ...if pozwala na wykonanie bloku instrukcji także w przypadku, gdy badane wyrażenie ma wartość False (Fałsz). Służy do tego klauzula else.elif pozwalają w jednej instrukcji if badać wartości wielu wyrażeń. W jednej instrukcji if możesz użyć dowolnej liczby klauzul elif, jednak instrukcja if działa tylko do napotkania pierwszego prawdziwego warunku. To oznacza, że jeżeli klauzul elif będzie kilka, to zostaną wykonane instrukcje tylko jednej z nich, pierwszej, która spełni warunek.print("Program podaje, która z 2 podanych liczb jest większa")a = float(input("Podaj pierwszą liczbę: "))b = float(input("Podaj drugą liczbę: "))
if a > b: print("Liczba", a, "jest większa")elif a == b: print("Liczba", a, "jest równa", b)else: print("Liczba", b, "jest większa")
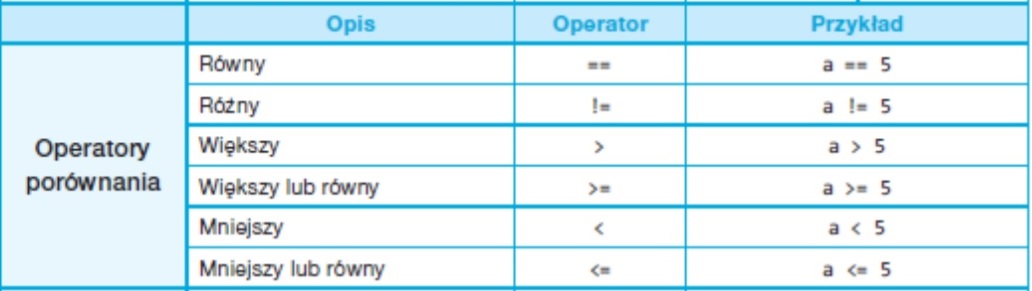
Operatory porównania wykorzystywane w instrukcji if
W tym programie zadeklarowałem zmienną x i przypisałem jej wartość 2. A dalej sprawdzam co się stanie jak wyświetlę na ekranie czy faktycznie x == 2 itd. True oznacza prawdę, a False fałsz. W komentarzach do instrukcji wyjścia print() napisałem czego się spodziewać. Zaznacz program i skopiuj do edytora Pythona. Sprawdź, co się dzieje.
x = 2print (x == 2) # wypisze True, bo przecież przypisałem wcześniej, że x = 2print (x != 2) # wypisze False, bo x nie może być różne od 2 skoro x = 2print (x == 3) # wypisze False, bo x nie może być równe 3 skoro jest równe 2print (x < 3) # wypisze True, bo 2 jest mniejsze od 3
Zmienne znacie już od dawna. Tworzyliśmy je w Scratchu np. po to żeby w grach wykorzystać licznik punktów.
Tworzeniezmiennych
Zmienna (ang. variable), to miejsce w pamięci komputera, w którym możemy zapisywać dane i do którego możemy mieć łatwy dostęp poprzez nadaną nazwę.
Tworzenie zmiennej w Pythonie polega na określeniu jej nazwy, oraz - po operatorze przypisania = podaniu danych, na które zmienna ma wskazywać, np.:
masa = 120
W taki sposób utworzyliśmy zmienną o nazwie masa i przypisaliśmy do niej wartość 120.
Nazwy zmiennych
Zmiennych można używać w wyrażeniach, w funkcji print(), np.:
masa = 10
print( masa * 2 )
20
Wymyślając nazwy zmiennych w Twoich programach pamiętaj o następujących regułach:
► nazwy mogą się składać tylko z liter, cyfr i znaku podkreślenia _
► nazwy nie mogą zawierać spacji
► nazwy nie mogą zaczynać się od cyfry
► wielkość liter ma znaczenie, tzn. zmienna masa to inna zmienna niż Masa
Poza tymi żelaznymi zasadami, warto stosować się do poniższych konwencji:
Poniżej znajduje się lista zastrzeżonych słów kluczowych, które nie mogą być nazwami zmiennych w Pythonie.
'False', 'None', 'True', 'and', 'as', 'assert', 'break', 'class', 'continue', 'def', 'del', 'elif', 'else', 'except', 'finally', 'for', 'from', 'global', 'if', 'import', 'in', 'is', 'lambda', 'nonlocal', 'not', 'or', 'pass', 'raise', 'return', 'try', 'while', 'with', 'yield'
Zmienne w wyrażeniach
Do zmiennych możesz przypisywać wartości wyrażeń, także takich, w których są inne zmienne, np.:
droga = 45
czas = 15
predkosc = droga / czas
print (predkosc)
3
Instrukcję wejścia znacie ze Scratcha.

Zmiennej możemy nadać wartość za pomocą instrukcji przypisania, wprowadzając wartość z klawiatury po uruchomieniu programu. W tym celu stosujemy instrukcję wejścia - funkcję input()
Na przykład:
nazwisko = input(“Podaj nazwisko: ”)
Typy zmiennych cz. 1
Teksty
String jest sekwencją znaków, a zazwyczaj przechowują słowa, zdania.
Liczby
Liczby w Pythonie mogą być dwojakiego typu – int (integer = l. całkowita) i float (floating point number l. zmiennoprzecinkowa).
Liczbą typu int będzie 4, która jest liczbą całkowitą, natomiast 4.4 jest już liczbą z przecinkiem, czyli float.
Przykład instrukcji wejścia z jednoczesnym określeniem typu zmiennej:
liczba = int(input(“Podaj liczbę: “))

Na lekcjach i w domu korzystamy z edytora Mu https://codewith.mu/